Local peak stresses are often relevant for crack initiation and usually occur at the welds. For the accurate fatigue assessment an objective and mesh independent stresses value is needed. In practice three different stress concepts are in use and most design codes refer to them. These are the nominal stress, the structural stress and the local notch stress.
- Nominal stress
- Structural stress
- Local notch stress
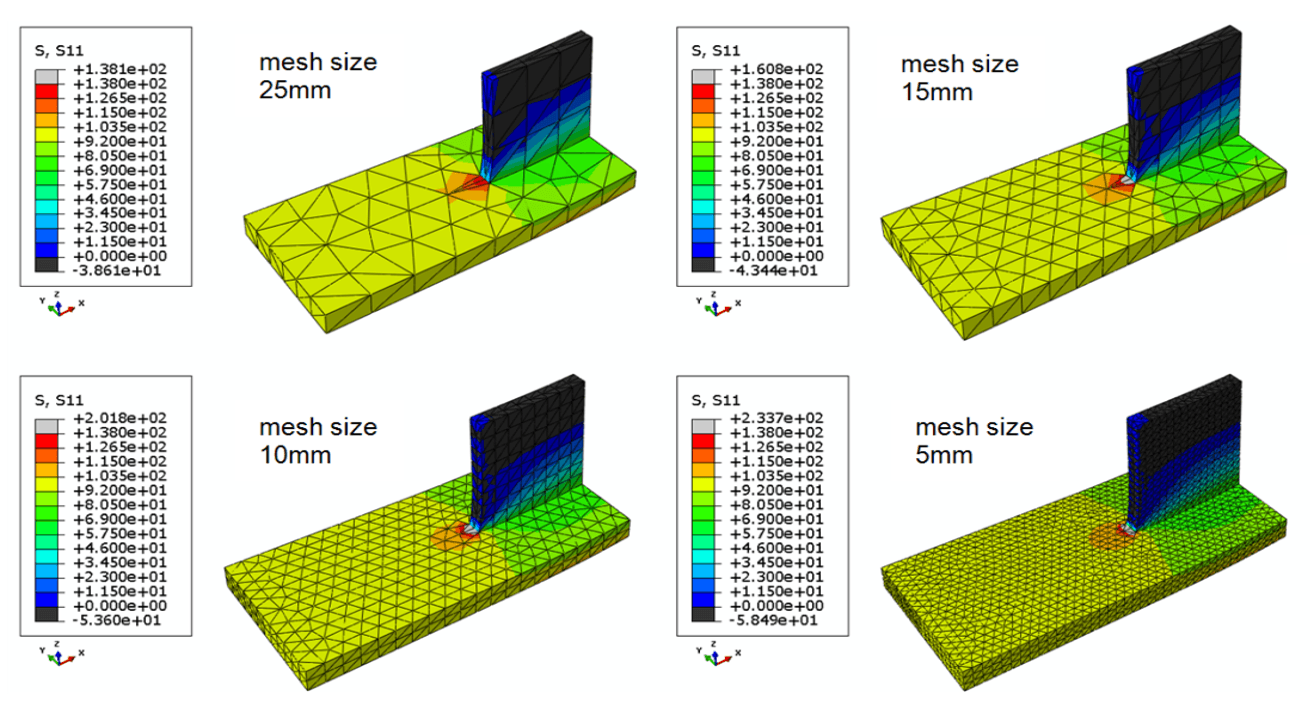
Changes in the structural stiffness usually coincide with local peak stresses. A typical example are the ends of an attached rib loaded in longitudinal direction of the weld. When analyzing such situations with the finite element method the numerical peak stress is strongly dependent on the element size, as shown in the following picture.
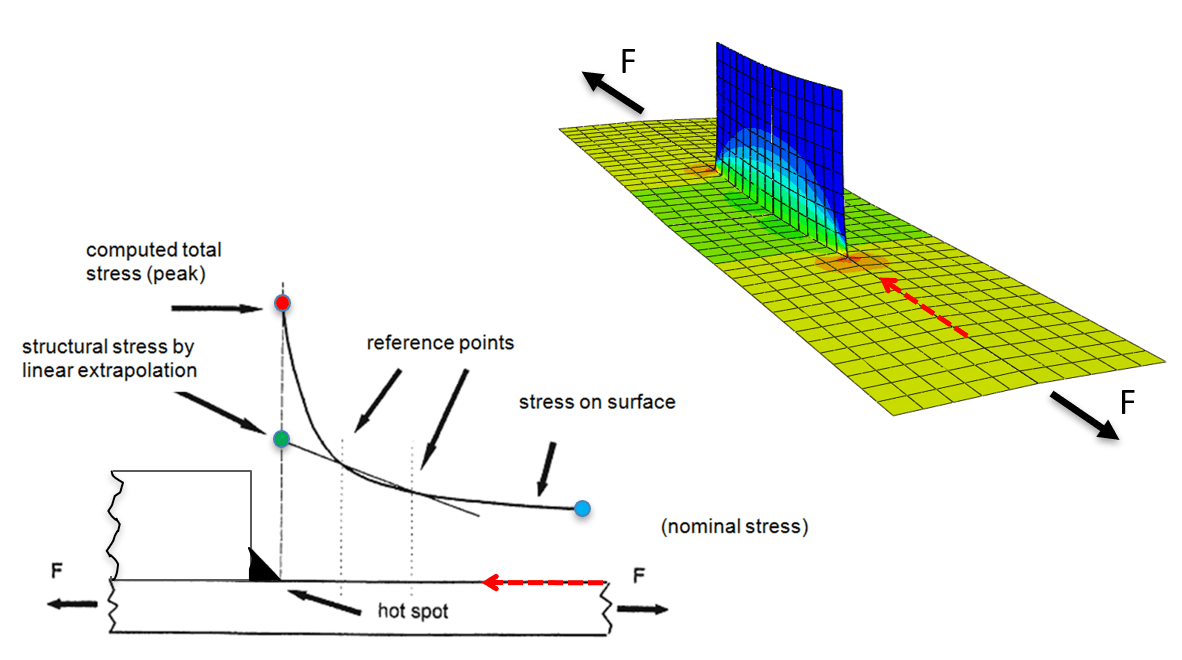
The differences of the three stress concepts are shown in the chart below. It shows the stress distribution depending on the distance from the corner point (hot spot). The nominal stress can be registered at the right end of the graph, far enough away the influence of the rib. No stress increase due to the rib is included. Approaching the hot spot the stress will increase until it reaches the peak value. If local notch stress models are used, the peak stress is meaning full and includes the structural stress increase as well as the increase at the weld toe. In any other case the peak stress is mesh dependent and cannot be used directly. The structural stress concept tries to capture the stress increase due to the rib (structural contribution) but excludes the local peak or singularity at the corner or at the weld toe. This is achieved using a stress extrapolation from the reference points.
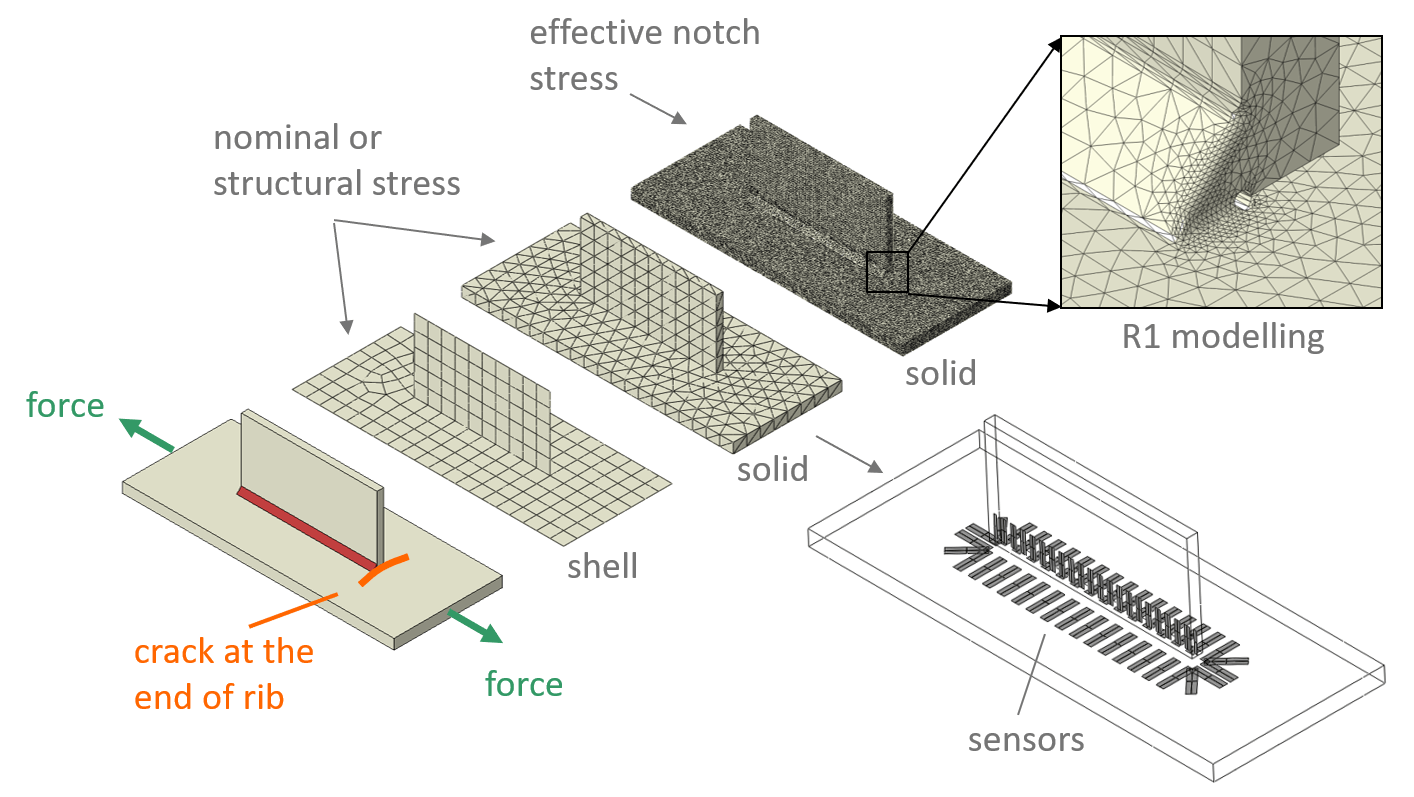
LIMIT® offers all three stress concepts. Local notch stress concepts are only possible with solid models. Nominal stress and structural stress concepts can be used for shell and solid models. The latter only in combination with Sensors. The following picture shows the three possible modeling approaches when using LIMIT.